Hồi quy dường như không liên quan SUR

Hồi quy dường như  không liên quan SUR ( SEEMINGLY UNRELATED REGRESSION), hướng dẫn hồi qui sur trên phần mềm stata, nhận biết khi nào dùng hồi quy có vẽ không liên quan, những điểm mấu chốt liên quan đến hồi quy sur và cách ứng dụng trong thực tế

SUR là gì ?

Trong kinh tế lượng , các hồi quy dường như không liên quan ( SUR )  hoặc phương trình hồi quy dường như không liên quan ( SURE )  , được đề xuất bởi Arnold Zellner vào năm 1962 , là một khái quát của mô hình hồi quy tuyến tínhbao gồm một số phương trình hồi quy, mỗi phương trình có biến phụ thuộc riêng và các bộ biến giải thích ngoại sinh khác nhau. Mỗi phương trình là một hồi quy tuyến tính hợp lệ và có thể được ước tính riêng, đó là lý do tại sao hệ thống được gọi là dường như không liên quan , mặc dù một số tác giả cho rằng thuật ngữ có vẻ liên quan sẽ phù hợp hơn,  vì các điều khoản lỗi được giả định là tương quan giữa các phương trình.

Mô hình có thể được ước tính phương trình theo phương trình bằng cách sử dụng bình phương tối thiểu thông thường (OLS) tiêu chuẩn . Các ước tính như vậy là phù hợp , tuy nhiên nhìn chung không hiệu quả như phương pháp SUR, tương đương với các bình phương tối thiểu tổng quát khả thi với một dạng cụ thể của ma trận phương sai – hiệp phương sai. Hai trường hợp quan trọng khi SUR trên thực tế tương đương với OLS là khi các thuật ngữ lỗi trên thực tế không tương quan giữa các phương trình (sao cho chúng thực sự không liên quan) và khi mỗi phương trình chứa chính xác cùng một bộ hồi quy ở phía bên phải.

Mô hình SUR có thể được xem như là sự đơn giản hóa của mô hình tuyến tính tổng quát trong đó các hệ số nhất định trong ma trận Beta được giới hạn bằng 0 hoặc là tổng quát hóa của mô hình tuyến tính tổng quát trong đó các biến hồi quy ở phía bên phải được phép khác nhau trong mỗi phương trình. Mô hình SUR có thể được khái quát hóa thành mô hình phương trình đồng thời , trong đó các biến hồi quy phía bên phải cũng được phép là các biến nội sinh.

Ứng dụng Seemingly unrelated regressions

Trong vấn đề kinh tế chúng ta giải quyết rất nhiều vấn đề phát sinh như: Hồi quy giả mạo -Giải quyết bằng cách tìm đồng liên kết, hay Vấn đề nội sinh trong mô hình kinh tế lượng – Giải quyết  bằng hồi quy GMM. Có một thực tế xảy ra, những vấn đề này điều giải quyết của biến độc lập còn biến phụ thuộc thì chưa giải quyết, đặc biệt là trong dự án chúng ta xây dựng nhiều mô hình nghiên cứu, với những trường hợp này chúng ta thường cho nó rời rạc với nhau hay còn gọi là không liên quan gì nhau, nhưng trong thực tế thì mọi vấn đề điều có tương quan với nhau; Vì vậy, nếu chúng ta không giải quyết vấn đề này thì hồi quy bình thường sẽ không còn chính xác nữa, Hồi quy dường như có vẻ liên quan SUR ra đời với mục đích giải quyết vấn đề trên.

Thực hành hồi quy SUR trên STATA

Để thực hành Hồi quy dường như không liên quan SUR chúng ta sử dụng bộ data sau:

use “C:\Users\Admin\Desktop\Vidu\survd.dta”

Mô hình nghiên cứu thứ1:

Điểm Đọc = Điểm Toán + Điểm Viết + Điểm Xã hội

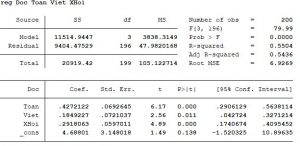
Từ kết quả trên ta có Điểm Toán + Điểm Viết + Điểm Xã hội điều có tác động đến Điểm Đọc, với mức ý nghĩa là 5%

Mô  hình nghiên cứu thứ 2:

Điểm KHoc = GioiTinh + Điểm Toán

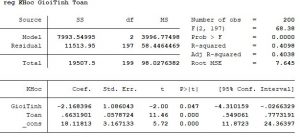
Chúng ta cũng có kết quả Giới Tính + Điểm Toán có ảnh hưởng đến Điểm KHoc, với mứ ý nghĩa 5%

Chúng ta kiểm tra tương quan của 2 mô hình:

Sau khi kiểm tra tương quan chúng ta dễ dàng nhận thấy rằng chúng có tương quan với nhau.

Hồi quy dường như không liên quan SUR

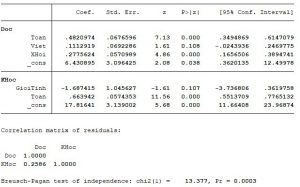
Sau khi hồi quy SUR:

• Đối với mô hình 1 chúng ta có thấy sự khác biệt: Điểm Viết không ảnh hưởng gì đến Điểm Đọc
• Đối với mô hình 2 có sự khác biệt: GioiTinh không ảnh hưởng đến điểm Khoa Học.

Sau khi hồi quy không liên quan SUR chúng ta có nhận thấy rằng, kết quả của mô hình SUR chính xác hơn nhiều và đúng với thực tế hơn mô hình hồi quy ols truyền thống.

Tổng quan

Người đánh giá

Hiểu

Ngày tương tác

2019-11-23

Lượng tương tác

Dễ hiểu mà

Tác giả đánh giá

5

Recipe Name

Hướng dẫn chạy mô hình định lượng