![[SVM] Thuật toán hỗ trợ máy vec-tơ Support vector machines](https://luanvanhay.org/wp-content/uploads/2022/09/svm5.png)
SVM Thuật toán hỗ trợ máy vec-tơ Support Vector Machines; Máy vectơ hỗ trợ còn được gọi là mạng vectơ hỗ trợ (SVN).
Máy vectơ hỗ trợ (SVM) là thuật toán máy học phân tích dữ liệu để phân loại và phân tích hồi quy. SVM là một phương pháp học có giám sát, xem xét dữ liệu và sắp xếp nó thành một trong hai loại. SVM xuất ra một bản đồ dữ liệu đã được sắp xếp với các lề giữa hai dữ liệu càng xa nhau càng tốt. SVM được sử dụng trong phân loại văn bản, phân loại hình ảnh, nhận dạng chữ viết tay và trong các ngành khoa học.
Support Vector Machines
Thuật toán hỗ trợ máy vector
Hỗ trợ Vector Machine hay SVM là một trong những thuật toán Học có Giám sát phổ biến nhất, được sử dụng cho các bài toán Phân loại cũng như Hồi quy. Tuy nhiên, chủ yếu, nó được sử dụng cho các vấn đề Phân loại trong Học máy.
Mục tiêu của thuật toán SVM là tạo đường hoặc ranh giới quyết định tốt nhất có thể tách không gian n chiều thành các lớp để chúng ta có thể dễ dàng đặt điểm dữ liệu mới vào đúng danh mục trong tương lai. Ranh giới quyết định tốt nhất này được gọi là siêu phẳng.
SVM chọn các điểm / vec-tơ cực hạn giúp tạo siêu phẳng. Những trường hợp cực đoan này được gọi là vec-tơ hỗ trợ, và do đó thuật toán được gọi là Máy vectơ hỗ trợ. Hãy xem xét sơ đồ dưới đây, trong đó có hai danh mục khác nhau được phân loại bằng cách sử dụng ranh giới quyết định hoặc siêu phẳng:
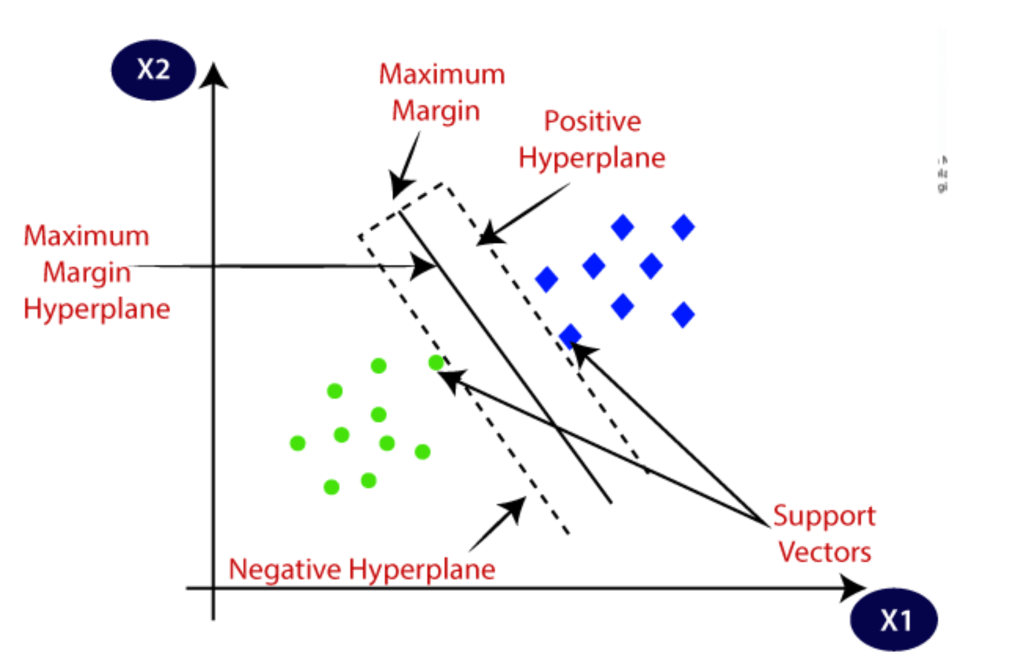
Giải thích về SVM
Máy vec-tơ hỗ trợ là một thuật toán học có giám sát để sắp xếp dữ liệu thành hai loại. Nó được đào tạo với một loạt dữ liệu đã được phân loại thành hai loại, xây dựng mô hình như nó được đào tạo ban đầu. Nhiệm vụ của thuật toán SVM là xác định loại điểm dữ liệu mới thuộc về loại nào. Điều này làm cho SVM trở thành một loại bộ phân loại tuyến tính không nhị phân.
Một thuật toán SVM không chỉ nên đặt các đối tượng vào các danh mục mà còn phải đặt lề giữa chúng trên một biểu đồ càng rộng càng tốt.
Một số ứng dụng của SVM bao gồm:
- Phân loại văn bản và siêu văn bản
- Phân loại hình ảnh
- Nhận dạng các ký tự viết tay
- Khoa học sinh học, bao gồm phân loại protein
Các loại thuật toán hỗ trợ máy vec-tơ
SVM có thể có hai loại:
- SVM tuyến tính: SVM tuyến tính được sử dụng cho dữ liệu có thể phân tách tuyến tính, có nghĩa là nếu một tập dữ liệu có thể được phân loại thành hai lớp bằng cách sử dụng một đường thẳng duy nhất, thì dữ liệu đó được gọi là dữ liệu có thể phân tách tuyến tính và bộ phân loại được sử dụng gọi là bộ phân loại SVM tuyến tính.
- SVM phi tuyến tính: SVM phi tuyến tính được sử dụng cho dữ liệu được phân tách không theo tuyến tính, có nghĩa là nếu tập dữ liệu không thể được phân loại bằng cách sử dụng một đường thẳng, thì dữ liệu đó được gọi là dữ liệu phi tuyến tính và bộ phân loại được sử dụng được gọi là Không bộ phân loại SVM tuyến tính.
Siêu phẳng và Vectơ hỗ trợ trong thuật toán SVM:
Siêu phẳng: Có thể có nhiều đường / ranh giới quyết định để phân tách các lớp trong không gian n chiều, nhưng chúng ta cần tìm ra ranh giới quyết định tốt nhất giúp phân loại các điểm dữ liệu. Ranh giới tốt nhất này được gọi là siêu phẳng của SVM.
Kích thước của siêu phẳng phụ thuộc vào các tính năng có trong tập dữ liệu, có nghĩa là nếu có 2 đặc điểm (như trong hình) thì siêu phẳng sẽ là một đường thẳng. Và nếu có 3 đặc điểm thì siêu phẳng sẽ là mặt phẳng 2 chiều.
Chúng tôi luôn tạo siêu phẳng có lề tối đa, nghĩa là khoảng cách tối đa giữa các điểm dữ liệu.
Hỗ trợ Vectơ:
Các điểm dữ liệu hoặc vectơ gần nhất với siêu phẳng và ảnh hưởng đến vị trí của siêu phẳng được gọi là Vectơ hỗ trợ. Vì những vectơ này hỗ trợ siêu phẳng, do đó được gọi là vectơ Hỗ trợ.
SVM hoạt động như thế nào?
SVM tuyến tính:
Hoạt động của thuật toán SVM có thể được hiểu bằng cách sử dụng một ví dụ. Giả sử chúng ta có một tập dữ liệu có hai thẻ (xanh lá cây và xanh lam), và tập dữ liệu có hai đặc điểm x1 và x2. Chúng tôi muốn một bộ phân loại có thể phân loại cặp tọa độ (x1, x2) theo màu xanh lục hoặc xanh lam. Hãy xem xét hình ảnh dưới đây:
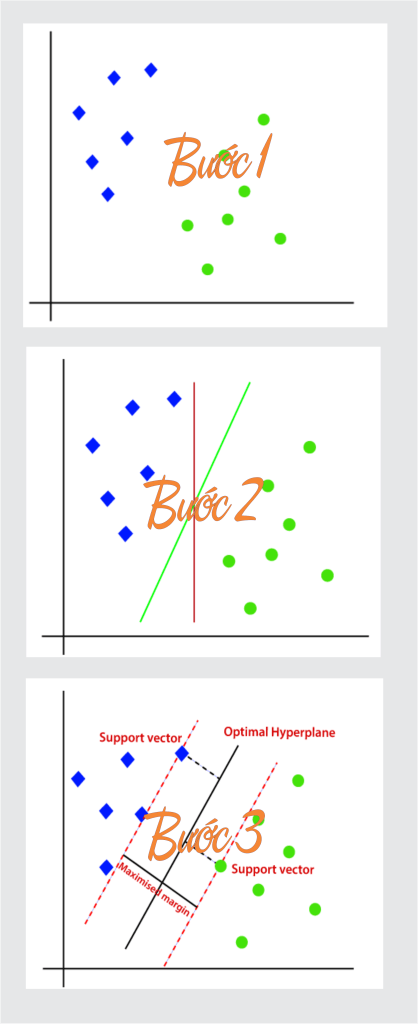
Vì nó là không gian 2 chiều nên chỉ cần sử dụng một đoạn thẳng, chúng ta có thể dễ dàng tách hai lớp này. Nhưng có thể có nhiều dòng có thể phân tách các lớp này. Hình nó như hình 2.
Do đó, thuật toán SVM giúp tìm đường hoặc ranh giới quyết định tốt nhất; ranh giới hoặc vùng tốt nhất này được gọi là siêu phẳng . Thuật toán SVM tìm điểm gần nhất của các dòng từ cả hai lớp. Những điểm này được gọi là vectơ hỗ trợ. Khoảng cách giữa các vectơ và siêu phẳng được gọi là lề . Và mục tiêu của SVM là tối đa hóa tỷ suất lợi nhuận này. Siêu phẳng với lợi nhuận tối đa được gọi là siêu phẳng tối ưu .
SVM phi tuyến tính:
Nếu dữ liệu được sắp xếp tuyến tính, thì chúng ta có thể tách nó ra bằng cách sử dụng một đường thẳng, nhưng đối với dữ liệu phi tuyến tính, chúng ta không thể vẽ một đường thẳng duy nhất. Như hình bước 1:
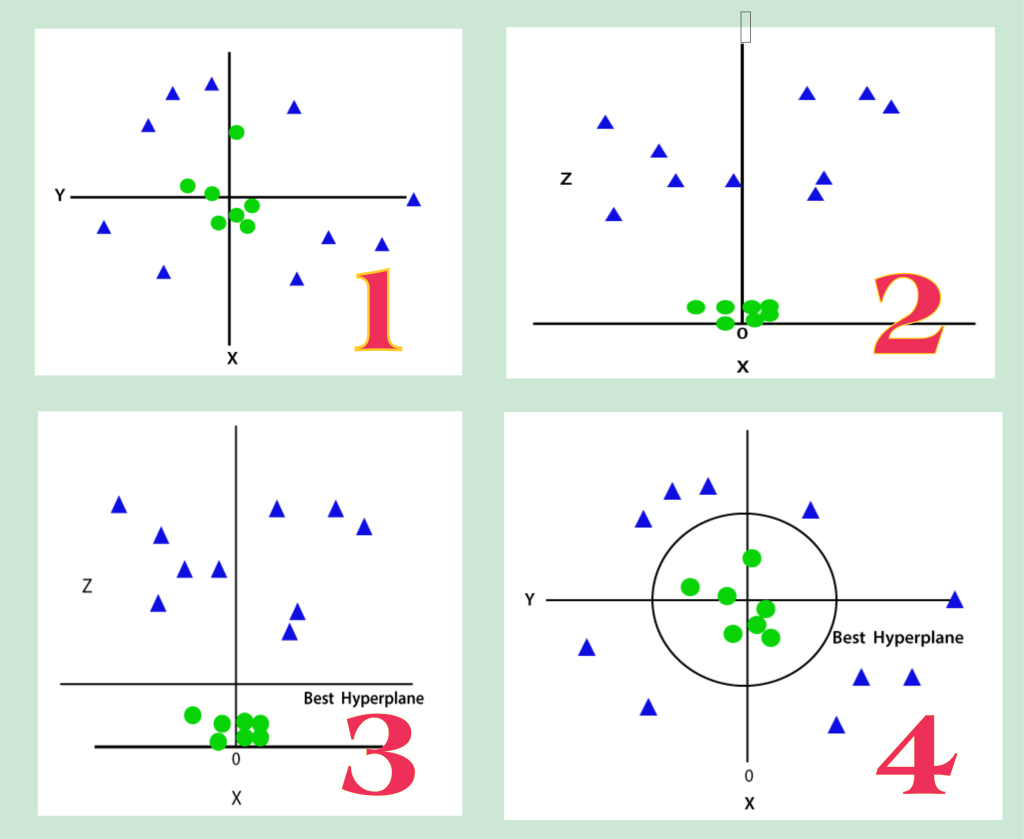
Vì vậy, để tách các điểm dữ liệu này, chúng ta cần thêm một thứ nguyên nữa. Đối với dữ liệu tuyến tính, chúng tôi đã sử dụng hai thứ nguyên x và y, vì vậy đối với dữ liệu phi tuyến tính, chúng tôi sẽ thêm thứ nguyên thứ ba z. Nó có thể được tính như sau:
z = x 2 + y 2
Bằng cách thêm kích thước thứ ba, không gian mẫu sẽ trở thành như hình ảnh bước 2.
Vì vậy, bây giờ, SVM sẽ chia các tập dữ liệu thành các lớp theo cách sau. Hãy xem xét hình ảnh bước3
Vì chúng ta đang ở trong Không gian 3-d, do đó nó trông giống như một mặt phẳng song song với trục x. Nếu chúng ta chuyển đổi nó trong không gian 2d với z = 1, thì nó sẽ trở thành như hình ảnh bước 4.
![[SPSS] Hồi quy đa thức Multinomial Logistic Regression](https://luanvanhay.org/wp-content/uploads/2022/09/dathuc6-FILEminimizer.png)
