Hồi quy quantile regression phân vị là một loại phân tích hồi quy được sử dụng trong thống kê và kinh tế lượng. Trong khi phương pháp bình phương tối thiểu ước tính giá trị trung bình có điều kiện của biến trả lời trên các giá trị của biến dự báo, hồi quy lượng tử ước tính trung vị có điều kiện (hoặc các phân vị khác ) của biến phản ứng. Hồi quy lượng tử là một phần mở rộng của hồi quy tuyến tính được sử dụng khi các điều kiện của hồi quy tuyến tính không được đáp ứng.
Hồi quy Quantile Regression là gì ?
Phương pháp hồi quy phân vị được Koenker & Bassett giới thiệu lần đầu tiên năm 1978. Thay vì ước lượng các tham số của hàm hồi quy trung bình bằng phương pháp OLS, Koenker & Bassett (1978) đề xuất việc ước lượng tham số hồi quy trên từng phân vị của biến phụ thuộc để sao cho tổng chênh lệch tuyệt đối của hàm hồi quy tại phân vị τ của biến phụ thuộc là nhỏ nhất. Nói một cách khác, thay vì xác định tác động biên của biến độc lập đến giá trị trung bình của biến phụ thuộc, hồi quy phân vị sẽ giúp xác định tác động biên của biến độc lập đến biến phụ thuộc trên từng phân vị của biến phụ thuộc đó. Đồng thời những ưu điểm của phương pháp hồi quy phân vị với phương pháp OLS của hồi quy cổ điển để cho thấy ưu điểm của hồi quy phân vị và sự phù hợp của hồi quy phân vị trong những nghiên cứu về chênh lệch tiền lương, cũng như trong các nghiên cứu về bất bình đẳng trong xã hội.
Ưu và nhược điểm
Sau khi Koenker và Bassett (1978) giới thiệu mô hình hồi quy phân vị đầu tiên, rất nhiều các nghiên cứu được thực hiện sau đó nhằm khắc phục các nhược điểm, đồng thời mở rộng hồi quy phân vị. Ngày càng có nhiều các bài nghiên cứu ứng dụng hồi quy được thực hiện và công bố, cho thấy hồi quy phân vị đang ngày càng được hoàn thiện và ngày càng trở thành công cụ đắc lực trong nghiên cứu kinh tế. Theo Koenker (2005) và Hao & Naiman (2007), hồi quy phân vị có những ưu điểm như sau.
Ưu điểm hồi quy phân vị
- Thứ nhất, phương pháp hồi quy phân vị cho phép thể hiện một cách chi tiết về mối quan hệ giữa biến phụ thuộc và các biến độc lập trên từng phân vị của biến phụ thuộc, không phải chỉ xét mối quan hệ này trên giá trị trung bình như hồi quy OLS. Ưu điểm này thể hiện nhiều hàm hồi quy cho nhiều phân vị, cho thấy tác động khác nhau của biến độc lập X ứng với nhiều phân vị của biến phụ thuộc Y.
- Thứ hai, mặc dù các tính toán thực hiện trong hồi quy phân vị là phức tạp và khối lượng tính toán nhiều hơn trong OLS, nhưng với sự phát triển của toán học, thống kê học cộng với sự hỗ trợ của công nghệ thông tin thì những tính toán như quy hoạch tuyến tính, bootstrap, được thực hiện rất dễ dàng và nhanh chóng.
- Thứ ba, trong hồi quy OLS, các quan sát bất thường (outliers) thường được loại bỏ để ước lượng OLS không bị chệch. Trong khi đó, hồi quy phân vị có tính ổn định (robustness), không bị ảnh hưởng bởi sự hiện diện của các quan sát bất thường đó.
- Thứ tư, các kiểm định về tham số của hồi quy phân vị không dựa vào tính chuẩn của sai số. Hơn nữa, các kiểm định này không dựa trên bất kỳ một giả định nào về dạng phân phối của sai số hồi quy.
- Thứ năm, hồi quy phân vị đặc biệt phù hợp khi phân tích trên mô hình hồi quy có sự hiện diện của phương sai thay đổi hoặc trong mẫu số liệu mà hàm phân phối của biến phụ thuộc bất đối xứng quanh giá trị trung bình. Khi đó, hàm hồi quy phân vị trên các phân vị khác nhau sẽ có sự khác biệt rõ rệt, cho thấy tác động không giống nhau của biến độc lập đến biến phụ thuộc ở những phân vị khác nhau.
Nhược điểm của hồi quy Quantile Regression
Bên cạnh các ưu điểm đã được nêu trên, hồi quy phân vị vẫn còn một số nhược điểm như sau:
- Một là, các tính toán trong hồi quy phân vị phức tạp hơn so với OLS. Ví dụ như trong OLS, muốn tìm ước lượng tham số hồi quy sao cho tổng bình phương sai số là nhỏ nhất thì có thể áp dụng các công thức tìm cực trị của giải tích toán học như lấy đạo hàm riêng và giải hệ phương trình ứng với điều kiện cần của cực trị. Trong khi đó, ước lượng tham số của hồi quy phân vị thực hiện thông qua việc giải bài toán quy hoạch tuyến tính. Việc này sẽ khó khăn nếu không có sự hỗ trợ của máy tính.
- Hai là, phải thực hiện nhiều hàm hồi quy trên nhiều phân vị mới cho thấy được toàn diện sự tác động của biến độc lập đến biến phụ thuộc thay vì chỉ có một hàm hồi quy trung bình có điều kiện trong OLS.
- Ba là, việc áp dụng hồi quy phân vị cho các dạng hàm phi tuyến còn khá hạn chế. Các lý thuyết để xử lý tự tương quan hoặc nội sinh trong hồi quy phân vị còn chưa được phát triển hoàn thiện.
Ứng dụng hồi quy phân vị trên Stata
Giả thuyết
Chúng ta xây dựng mối quan hệ của CPI + DC tác động lên LnGDP, thường mối quan hệ tác động như thế này thì chúng ta sẽ dễ dàng phân tích bằng hồi quy bình phương nhỏ nhất cũng cho ra kết quả tương ứng, nhưng có một sự thật là hồi quy ols chỉ cho ra kết quả trung bình của CPI + DC tác động lên LnGDP,không nói lên được mức độ của CPI DC tác động lên LnGDP khi tăng trưởng 10 % | 25% | 50% | 75% | 90% sẽ như thế nào ? với giả thuyết này thì chúng ta hồi quy phân vị để nhận biết mức độ của CPI + DC ảnh hưởng lên từng phân vị của LnGDP như thế nào ?
Hồi quy phân vị
Kết quả hồi quy với các phân vị trên, ta được:
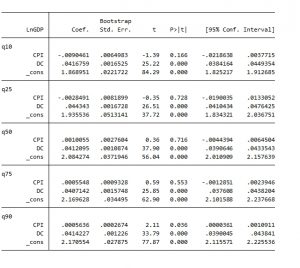
CPI: Ta có được được tuy không có ý nghĩa thống kê nhưng hệ số tác động của CPI thay đổi liên tục, nếu hệ số phân vị < 50% thì có hệ số tác động là âm lên biến phụ thuộc, nhưng khi hệ số phân vị > 50% thì ngược lại, nó có tác động dương đến LnGDP. Và đặc biệt ở phân vị 90% thì biến CPI có ý nghĩa thống kê, tức là biến CPI có tác động dương lên biến phụ thuộc.
DC: Có ý nghĩa thống kê cho 5 phân vị, đồng thời chỉ khác nhau về hệ số tác động.
Kiểm định phương sai sai số thay đổi
ta có được phương sai sai số khi phân vị là 10% là cố định còn lại những phân vị khác là phương sai phần dư thay đổi
Machado-Santos Silva test for heteroskedasticity
Ho: Constant variance
Variables: Fitted values of LnGDP and its squares
chi2(2) = 4.996
Prob > chi2 = 0.082
Đồ thị phân vị
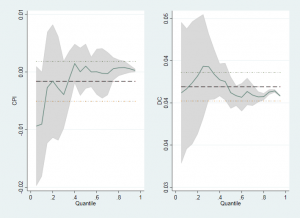
CPI: Qua đồ thị chúng ta dễ dàng thấy được rằng, khi phân vị càng thấp thì CPI tác động lên LnGDP càng ít, nhưng khi phân vị là 20% thì CPI có tác động dương với biến phụ thuộc, đồng thời khi tăng phân vị lên thì CPI cũng tăng dần mức độ ảnh hưởng lên LnGDP
DC: Khi phân vị tăng dần cho đến 30% thì DC có tác động cùng chiều với biến phụ thuộc, nhưng khi phân vị tăng hơn 30% thì DC có tác động ngược chiều với LnGDP.
Ứng dụng hồi quy phân vị
Theo Hao & Naiman (2007), hồi quy phân vị đặc biệt phù hợp với việc nghiên cứu chênh lệch tiền lương9, vì những lý do như sau:
Một là, trong nội dung nghiên cứu về chênh lệch tiền lương, ngoài yêu cầu phân tích chênh lệch tiền lương trung bình, các nhà nghiên cứu còn cần chú ý phân tích chênh lệch tiền lương trung bình ở nhóm tiền lương thấp, nhóm tiền lương cao và các nhóm khác từ thấp đến cao. Do đó, có thể vận dụng hồi quy phân vị ứng với các phân vị khác nhau để cho thấy mức độ chênh lệch theo từng nhóm tiền lương.
Hai là, hàm phân phối của biến tiền lương thường là hàm phân phối bất cân xứng, có dạng phân phối nặng đuôi (heavy – tailed), là điển hình của mẫu số liệu bị hiện tượng phương sai thay đổi. Phương pháp hồi quy quantile regression phân vị thích hợp với các mẫu số liệu có hiện diện hiện tượng phương sai thay đổi vì phương pháp này không những cho thấy tác động theo vị trí mà còn phân tích tác động theo quy mô của hàm phân phối.
Ba là, phương pháp hồi quy phân vị có thể thực hiện tại một mức phân vị bất kỳ t Î(0,1) Vì vậy, nếu có một nghiên cứu kinh tế hay một lý thuyết kinh tế nào đó công bố thông tin về bất bình đẳng tại một phân vị cụ thể nào đó, thì nhà nghiên cứu
có thể thực hiện hồi quy tại phân vị tương ứng để phân tích. Ví dụ, trong nghiên cứu về tình trạng đói nghèo tại Việt Nam cho thấy tỷ lệ hộ nghèo ở Việt Nam năm 2010 là 9,45% (theo Tổng cục Thống kê), khi thực hiện hồi quy phân vị có thể tiến hành hồi quy theo phân vị tương ứng với tỷ lệ này để có những kết luận phù hợp. Đây là điều không thể thực hiện được nếu dùng OLS.
Bốn là, phương pháp hồi quy phân vị về tiền lương có thể được thực hiện đối với nhiều phân vị (cách nhau 5% hoặc 1%). Do đó, có thể thấy được tác động của các yếu tố đến tiền lương ở từng phân vị khác nhau sẽ khác nhau như thế nào. Ứng với mỗi nhóm phân vị khác nhau có thể có những yếu tố tác động khác nhau. Từ đó, nhà nghiêu cứu có thể đề xuất các chính sách, các giải pháp cho phù hợp.
Năm là, các nghiên cứu về chênh lệch tiền lương, chênh lệch thu nhập, chênh lệch mức sống cũng như các nghiên cứu về tình trạng bất bình đẳng trong xã hội thường ít dựa trên các mô hình mà dựa trên các chỉ tiêu đo lường sự bất bình đẳng như đường cong Lorenz, hệ số Gini, chỉ số Theil… Với các ưu điểm nêu trên, hồi quy quantile regression phân vị được bổ sung vào kho công cụ để nghiên cứu sự bất bình đẳng như là một công cụ nghiên cứu thuận tiện và hiệu quả.



![[Mở lớp] Phân tích dữ liệu Stata Smartpls Amos R-studio SPSS Minitab NCSS](https://luanvanhay.org/wp-content/uploads/2023/05/huong-dan-6-120x86.jpg)





![[Mở lớp] Phân tích dữ liệu Stata Smartpls Amos R-studio SPSS Minitab NCSS](https://luanvanhay.org/wp-content/uploads/2023/05/huong-dan-6-360x180.jpg)








