khắc phục đa cộng tuyến bằng Ridge, Ridge là một phương thức hồi quy phi tuyến tính; Trong ví dụ này chúng ta không bàn về định nghĩa của các định nghĩa, nếu các bạn muốn quan tâm đến các định nghĩa vui lòng truy cập vào link trên; Chúng ta chỉ tập trung vào khắc phục đa cộng tuyến bằng phương pháp hồi quy ridge trên phần mềm thống kê R.
Trong thực tế khi nghiên cứu chúng ta thường bắt gặp hiện tượng đa cộng tuyến, đặc biệt là trong các nghiên cứu về kinh tế. đây là một sai phạm nghiêm trọng là cho ước lượng hồi quy của chúng ta bị chệch và không còn chính xác nữa ! Để nhận biết hiện tượng đa cộng tuyến trong mô hình nghiên cứu, chúng ta dùng chỉ số VIF là chính xác nhất, không dùng hệ số tương quan hay R2.
VIF là gì ?
Trong thống kê , hệ số lạm phát phương sai (Variance inflation factor – VIF ) là thương số của phương sai trong một mô hình có nhiều số hạng bằng phương sai của một mô hình chỉ có một thuật ngữ. Nó định lượng mức độ nghiêm trọng của đa cộng tuyến trong phân tích hồi quy bình phương nhỏ nhất bình thường . Nó cung cấp một chỉ số đo lường mức độ chênh lệch (bình phương độ lệch chuẩn của ước tính) của một hệ số hồi quy ước tính được tăng lên do cộng tuyến.
Ta có công thức tính VIF như sau:
HOT:
VIF = 1/ (1-R2)
Mối tương quan giữa VIF với R2
Mối quan hệ này được khái quát trong bảng sau:
| R2 | VIF |
| 0.1 | 1.010101 |
| 0.2 | 1.041667 |
| 0.3 | 1.098901 |
| 0.4 | 1.190476 |
| 0.5 | 1.333333 |
| 0.6 | 1.5625 |
| 0.7 | 1.960784 |
| 0.8 | 2.777778 |
| 0.9 | 5.263158 |
| 0.91 | 5.817336 |
| 0.92 | 6.510417 |
| 0.93 | 7.401925 |
| 0.94 | 8.591065 |
| 0.95 | 10.25641 |
| 0.96 | 12.7551 |
| 0.97 | 16.92047 |
| 0.98 | 25.25253 |
| 0.99 | 50.25126 |
Khi chúng ta có hệ số xác định R2 >90, thì đây là một cách để nhận biết trong mô hình nghiên cứu của chúng ta đang có hiện tượng đa cộng tuyến, nếu chúng ta không có biện pháp nào khác phụ thì kết quả hồi quy sẽ không còn chính xác nữa.
Tùy vào nhiều nghiên cứu và có mức độ xét đa tuyến tính dễ hay khắc khe, nó sẽ nằm trong 2 mức:
- VIF < 5: Không có hiện tượng đa cộng tuyến
- VIF < 10 Không có hiện tượng đa cộng tuyến
Trong ví dụ tiếp theo, chúng ta sử dụng mức xét collinearity dễ tức VIF <10
Mối tương quan giữa cor với VIF
Có một số tài liệu của VN chúng ta nói rằng hệ số tương quan cor>0.6 là có hiện tượng đa cộng tuyến, vấn đề này mình khẳng định với các bạn là chưa đủ căn cứ để khẳng định sai phạm trong mô hình; trong bài viết này chúng tôi chỉ tập trung với mối quan hệ của VIF với R2 còn mối quan hệ giữa COR với R2 chúng tôi hẹn vào bài viết khác.
Đa cộng tuyến là gì ?
Trong thống kê , multicollinearity (cũng là collinearity ) là một hiện tượng trong đó một biến dự báo trong mô hình hồi quy bội có thể được dự đoán tuyến tính từ các biến khác với độ chính xác đáng kể. Trong tình huống này, các ước tính hệ số của hồi quy bội có thể thay đổi thất thường để đáp ứng với những thay đổi nhỏ trong mô hình hoặc dữ liệu. Multicollinearity không làm giảm sức mạnh dự đoán hoặc độ tin cậy của toàn bộ mô hình, ít nhất là trong tập dữ liệu mẫu; nó chỉ ảnh hưởng đến các tính toán liên quan đến các yếu tố dự đoán riêng lẻ. Đó là, một mô hình hồi quy đa biến với các yếu tố dự đoán cộng tuyến có thể cho biết toàn bộ gói dự đoán biến dự đoán kết quả tốt như thế nào , nhưng nó có thể không đưa ra kết quả hợp lệ về bất kỳ dự đoán riêng lẻ nào, hoặc về dự đoán nào là dự phòng đối với người khác.
Lưu ý rằng trong các tuyên bố về các giả định cơ bản phân tích hồi quy như bình phương tối thiểu thông thường , cụm từ “không có đa cộng tuyến” thường đề cập đến sự vắng mặt của đa hình hoàn hảo , đó là mối quan hệ tuyến tính chính xác (không ngẫu nhiên) giữa các yếu tố dự đoán. Trong trường hợp đó, ma trận dữ liệu X có ít hơn thứ hạng đầy đủ , và do đó ma trận thời điểm X T X không thể đảo ngược . Trong những trường hợp này, cho một mô hình tuyến tính nói chung y = Xβ +ε, công cụ ước lượng bình phương nhỏ nhất βols = (X T X)-1 XTy không tồn tại.
Trong mọi trường hợp, tính đa hướng là một đặc tính của ma trận dữ liệu, không phải là mô hình thống kê cơ bản . Vì nó thường nghiêm trọng hơn trong các mẫu nhỏ, Arthur Goldberger đã đi xa đến mức gọi nó là “vi mô”.
Bài thực hành
Thực hành tìm và khắc phục hiện tượng đa cộng tuyến trên R
Tìm hiện tượng đa cộng tuyến trong dữ liệu
Chúng ta có mô hình nghiên cứu như sau:
ROE = LnSIZE + LnEQAS + LnCP + INF
Chúng ta ước lượng hồi quy ols và thu được kết quả như sau:
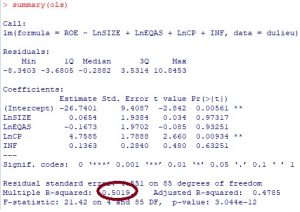
Ta thu được kết quả R2 = 0.5019, tra vào bảng tương quan trên thì chúng ta sẽ dễ dàng bị nhầm lẫn, kết luận vội vàng là trong mô hình nghiên cứu của chúng ta không có hiện tượng multicollinearity; Bây giờ chúng ta tìm hàm VIF xem kết quả như thế nào.
vif(ols)
LnSIZE LnEQAS LnCP INF
13.179941 11.992100 12.628649 1.027252
Ta ta dễ dàng nhận thấy rằng có 3 biến có VIF > 10 đó là: LnSIZE LnEQAS LnCP; Đối chiếu vào kết quả trên là chúng ta nhận thấy rằng kết quả đã có sự mẫu thuẫn. Điều này chúng tỏ dùng R2 để nhận định VIF là hoàn toàn sai lầm.
Khắc phục đa cộng tuyến bằng hồi quy Ridge
Tìm Lambda theo điều kiện
Như chúng ta đã biết mô hình Ridge dùng hệ số lambda để điều chỉnh hệ số hồi quy, nếu λ = 0 thì hồi quy ridge thành hồi quy ols. Ta ước lượng hồi quy Ridge và được bảng lambda sau:
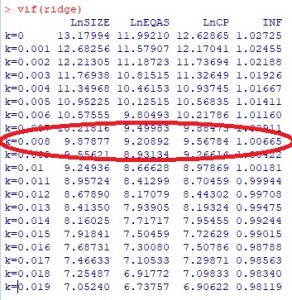
Ta có kết luận rằng khi lambda >= 0.008 thì mô hình không còn hiện tượng đa cộng tuyến, Vì tất cả hệ số VIF điều nhỏ hơn 10.
Tìm λ tối ưu cho mô hình
Để cho mô hình tối ưu thì có rất nhiều chỉ tiêu nhứ: AIC, BIC, R2, MSE, RMSE …
Trong ví dụ này chúng tôi sử dụng mô hình MSE để tìm lambda tối ưu
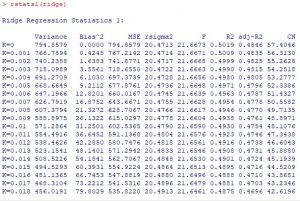
Tra trong bảng trên ta có MSE nhỏ nhất là 502.852 tại lambda = 0.033
Đồng thời lambda > 0.008, ta chấp nhận giá trị lambda này.
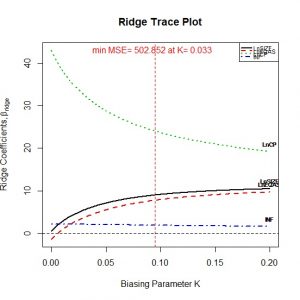
Hồi quy Ridge với kết quả λ tối ưu
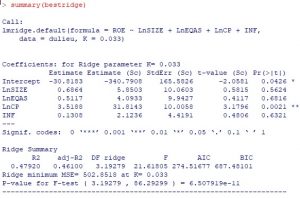
Đây là kết quả của chúng sau khi đã khắc phục hiện tượng đa cộng tuyến; Để cho chắc ăn kiểm tra lại hệ số VIF từng phần một lần nữa xem sao.
vif(bestridge)
LnSIZE LnEQAS LnCP INF
k=0.033 4.93279 4.81807 4.87948 0.95177
Chúng ta thấy rằng hệ số VIF của chúng điều < 5, như vậy trong mô hình không có hiện tượng đa cộng tuyến.
Hồi quy Ridge khắc phục sai phạm đa cộng tuyến
Sai phạm về đa cộng tuyến là một sai phạm rất lớn trong quá trình nghiên cứu định lượng, trước đây cũng có nhiều phương pháp đề ra để khắc phục hiện tượng này, nhưng tính thuyết phụ không cao, chúng ta thường dùng phương pháp chấp nhận đa cộng tuyến, hơn mở rộng thêm dữ liệu, nhằm hạn chế đa cộng tuyến trong mô hình; Với vấn đề áp dụng phương cách hồi quy phi tuyến hay ví dụ thực tế là hồi quy ridge đã khắc phục hiện tượng đa cộng tuyến dễ dàng.
Cảm ơn các bạn đã đọc tin.
