Hiệu quả kỹ thuật bởi Phân tích biên ngẫu nhiên, hướng dẫn tính hiệu quả phi kỹ thuật trên các mô hình kinh tế quan trọng như Cobb-Douglas hay Translog, phương pháp SFA được áp dụng rộng rãi để tính Hiệu quả kỹ thuật, Tiến bộ công nghệ, Hiệu quả môi trường … Trong bài này chúng tôi sẽ hướng dẫn cho các bạn tính hiệu quả kỹ thuật trên mô hình kinh tế cụ thể được ứng dụng cụ tại một tỉnh cụ thể, giúp cho các bạn dễ dàng hình dung được mô hình Phân tích biến ngẫu nhiên. Trong ví dụ này, chúng tôi ước lượng TE trên phần mềm thống kê R.
SFA là gì?
Phân tích biên ngẫu nhiên (SFA – Stochastic frontier analysis) đề cập đến một nhóm các kỹ thuật phân tích thống kê được sử dụng để ước tính các hàm sản xuất hoặc chi phí trong kinh tế, trong khi tính toán rõ ràng cho sự tồn tại của sự kém hiệu quả của công ty. Từ hoạt động trong định nghĩa này là không hiệu quả, ngụ ý các nhà sản xuất có thể hành xử dưới mức tối ưu trong các quyết định của họ để tối đa hóa hoặc giảm thiểu một số chức năng khách quan (ví dụ: lợi nhuận, sản xuất, doanh thu hoặc chi phí). Nền tảng trí tuệ của sự kém hiệu quả trong kinh tế học có thể bắt nguồn từ các tác phẩm của John Hicks (1938), người cho rằng các nhà độc quyền sở hữu những động lực khác hơn là tối đa hóa lợi nhuận thuần túy; những động lực này có thể dẫn đến sản xuất dưới mức tối ưu. (Xem Kumbhakar và Lovell [2000] để biết các cách hợp lý hóa khác cho sự không hiệu quả trong trạng thái cân bằng và một cuộc thảo luận về nền tảng trí tuệ của nó.)
Xây dựng công thức Phân tích biên ngẫu nhiên SFA:
Phương pháp SFA cho phép đánh giá hiệu quả kỹ thuật và giải quyết một số vấn đề liên quan đến các mô hình định lượng của hàm biên, có tính đến các nhân tố đi kèm ảnh hưởng ngẫu nhiên đến quá trình sản xuất, do đó kết quả của SFA cũng mang tính ngẫu nhiên. Phương pháp SFA lần đầu tiên được đề xuất vào năm 1977 bởi hai nhóm tác giả độc lập là Aigner, Lovell và Schmidt, và nhóm Meeusen, Van den Broeck. Mô hình phân tích SFA được tóm gọn như sau:
Yi = f(Xi;B)exp(Vi-Ui)
Yi: là biến đầu ra
Xi: Là các biến đầu vào
Vi: Là sai số ngẫu nhiên độc lập, đồng nhất và đối xứng với mô hình; nó đại diện cho tác động nhiễu ngoài tầm kiểm soát như: thời tiết, sự may rủi, sai số thống kê …
Ui: Hiệu quả phi kỹ thuật
Vài định nghĩa liên quan tới Stochastic frontier analysis
Efficiency: Khái niệm về hiệu quả
Hiệu quả là sự liên quan giữa nguồn lực đầu vào khan hiếm (như lao động, vốn, máy móc thiết bị,…) với kết quả trung gian hay kết quả cuối cùng. Hiểu theo nghĩa rộng, hiệu quả thể hiện mối tương quan giữa các biến số đầu ra thu được (outputs) so với các biến số đầu vào (inputs) đã được sử dụng để tạo ra những kết quả đầu ra đó.
Hiệu quả = Đầu ra /Đầu vào
Technical efficiency: Hiệu quả kỹ thuật
Theo nhà kinh tế học người Anh M. Farrell (1957), hiệu quả hoạt động (operational effi ciency) được chia làm 2 phần: 1) Hiệu quả kỹ thuật hoặc hiệu quả sản xuất (technical efficiency); và 2) Hiệu quả phân phối nguồn lực (allocative efficiency). Hiệu quả kỹ thuật là tối thiểu hóa lượng các yếu tố đầu vào với đầu ra cho trước hoặc tối đa hóa các yếu tố đầu ra với lượng yếu tố đầu vào cho trước .
TE = exp(-Ui) = exp(XiB+Vi-Ui)/exp(XiB+Vi)=Y/Y*
Bài mới !
điều kiện: TE<=1
Các phương thức ước lượng hiện quả kỹ thuật (TE):
SFA:
Mô hình biên giới ngẫu nhiên lần đầu tiên được đề xuất trong bối cảnh ước tính hàm sản xuất để tính đến hiệu quả của sự kém hiệu quả kỹ thuật. Sự kém hiệu quả làm cho sản lượng thực tế giảm xuống dưới mức tiềm năng (nghĩa là biên giới sản xuất) và cũng làm tăng chi phí sản xuất trên mức tối thiểu (nghĩa là biên giới chi phí). Các ứng dụng gần đây của mô hình được tìm thấy trong nhiều lĩnh vực nghiên cứu bao gồm lao động, tài chính và tăng trưởng kinh tế. Trong các ứng dụng này, kết quả quan sát được (về tiền lương, đầu tư, v.v.) được mô hình hóa là đi chệch khỏi cấp độ biên giới theo một hướng do các yếu tố như sự bất cân xứng thông tin.
DEA:
Data Envelopment Analysis : Phân tích bao bọc dữ liệu là một phương pháp không tham số trong nghiên cứu hoạt động và kinh tế để ước tính biên giới sản xuất . Nó được sử dụng để đo lường thực nghiệm hiệu quả sản xuấtcủa các đơn vị ra quyết định (DMU). Mặc dù DEA có mối liên hệ chặt chẽ với lý thuyết sản xuất trong kinh tế học, công cụ này cũng được sử dụng để đo điểm chuẩn trong quản lý hoạt động, trong đó một bộ các biện pháp được chọn để đánh giá hiệu suất của hoạt động sản xuất và dịch vụ. Trong điểm chuẩn, các DMU hiệu quả, như được định nghĩa bởi DEA, có thể không nhất thiết phải tạo thành một biên giới sản xuất, mà là dẫn đến một biên giới thực hành tốt nhất của Anh (Cook, Tone và Zhu, 2014). DEA được gọi là “điểm chuẩn cân bằng” của Sherman và Zhu (2013).
Trong ví dụ này chúng tôi sử dụng phương pháp Phân tích biên ngẫu nhiên SFA.
Các bước ước lượng Hiệu quả kỹ thuật
Lựa chọn hàm Cobb-Douglas hay Translog
Mô hình nghiên cứu của chúng ta như sau: GDP = K + L
Trong đó:
- GDP: Tổng gdp của tỉnh A
- K: Tổng vốn của tỉnh A
- L: Tổng lao động của tỉnh A
- i: các năm
Ta xây dựng hàm Cobb-Douglas như sau:
LnGDP = LnK + LnL (model1)
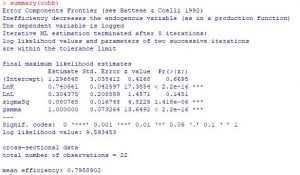
Đồng thời ta cũng xây dựng hàm Translog như sau:
LnGDP = LnK + LnL + LnKL + LnK2 + LnL2 (model2)
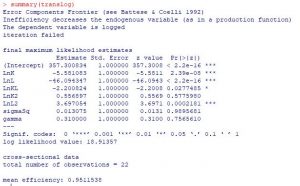
Chúng ta tính chỉ số LR
LR= -2(LH0 – LH1)= -2(9.6-18.9)=28.2
Tiếp theo chúng ta tính giá trị Chi2 tại bậc 3:
chi2(0.95,3)=7.8
Nếu bạn gặp khó khăn trong việc tính toán giá trị Chi2, các bạn có thêm tra bảng thống kê chi2
Ta đặt giả thuyết như sau:
- H0: Mô hình Cobb-Douglas là phù hợp để ước lượng
- H1: Mô hình Cobb-Douglas không phù hợp để ước lược.
Ta có LR > Chi2 => Tức là chúng ta bác bỏ H0 chấp nhận H1, tức là mô hình Translog phù hợp hơn để ước lượng.
Kiểm định hiện tượng hiểu quả phi kỹ thuật
Đây còn gọi là 1 phương thức lựa chọn phương pháp để ước lượng Phân tích biên ngẫu nhiên giữa OLS với MLS.
Tao có gama =0.31 => Mô hình có hiện tượng Hiệu quả phi kỹ thuật, vì vậy chúng ta ước lượng MLS là hợp lý nhất.
Kiểm định Hiệu quả phi kỹ thuật là bán chuẩn.
Bán chuẩn là gì?
Trong lý thuyết xác suất và thống kê, phân phối bán chuẩn là trường hợp đặc biệt của phân phối chuẩn gấp .
Để cho theo một phân phối bình thường bình thường ,, sau đó theo một phân phối nửa bình thường. Do đó, phân phối nửa bình thường là một nếp gấp tại giá trị trung bình của phân phối chuẩn thông thường với giá trị trung bình bằng 0.
Phân phối chuẩn gấp là gì?
Các phân phối bình thường gấp là một phân bố xác suất liên quan đến việc phân phối chuẩn . Cho một phân bố bình thường ngẫu nhiên biến X với trung bình μ và phương sai σ 2 , các biến ngẫu nhiên Y = | X | có một phân phối bình thường gấp. Một trường hợp như vậy có thể gặp phải nếu chỉ ghi lại cường độ của một số biến, nhưng không phải là dấu hiệu của nó. Phân phối được gọi là “gấp” vì khối lượng xác suất ở bên trái của x = 0 được gấp lại bằng cách lấy giá trị tuyệt đối .
Đọc mấy cái đinh nghĩa này nhứt đầu lắm, xem hình ảnh là dễ hiểu nhất
Để cho dễ hiểu, các bạn đã biết phân phối chuẩn là hình chung rồi, bây giờ bán chuẩn là chia đôi hình chuông ra thôi. Nói chung là nữa hình chuông thôi ( Nhớ chẻ dọc đừng chẻ ngang).
Kết luận:
Sau khi thực hiện qua nhiều bước thì chúng ta có thể ước lượng được giá trị TE ( Hiệu quả kỹ thuật) một cách đơn giản. Chúng ta có Giá trị TE trung bình qua các năm tại tỉnh A là: 95.11%.
Cảm ơn các bạn đã đọc bài !
