mô hình tự hồi quy var trên eviews, hướng dẫn cách hồi quy var – Vector autoregression, đây là một mô hình hiện đại được ứng dụng nhiều trong dự báo các chỉ số có độ nhạy cao như: chỉ số cpi, chỉ số lạm phát, giá cả, chỉ số index, giá vàng, giá dầu …. Chúng là công cụ được các nhà kinh tế sử dụng nhiều và rất nhiều trong dự báo kinh tế.
Mô hình tự hồi quy var là gì ?
Vector autorewardsion ( VAR ) là một mô hình quy trình ngẫu nhiên được sử dụng để nắm bắt các phụ thuộc tuyến tính giữa các chuỗi thời gian . Các mô hình VAR tổng quát hóa mô hình tự phát đơn biến (mô hình AR) bằng cách cho phép nhiều hơn một biến phát triển. Tất cả các biến trong VAR nhập mô hình theo cùng một cách: mỗi biến có một phương trình giải thích sự tiến hóa của nó dựa trên các giá trị bị trễ của chính nó , các giá trị bị trễ của các biến mô hình khác và một thuật ngữ lỗi . Mô hình hóa VAR không đòi hỏi nhiều kiến thức về các lực ảnh hưởng đến một biến như các mô hình cấu trúc với các phương trình đồng thời: Kiến thức duy nhất cần có là một danh sách các biến có thể được đưa ra giả thuyết để ảnh hưởng lẫn nhau.
Giải quyết vấn đề trong mô hình hồi quy OLS
Trong hồi quy bình phương nhỏ nhất hay là hồi quy cổ định, chúng ta chỉ có được biến độc lập làm ảnh hưởng đến biến phụ thuộc, trong nhiều trường nhiều ngoài chuyện biến độc lập ảnh hưởng lên biến phụ thuộc và còn biến phụ thuộc ảnh hưởng ngược lại biến độc lập, vì vậy chúng ta phải sử dụng mô hình tự hồi quy var để ước lượng sự ảnh hưởng của chúng.
Hiện tại ngoài mô hình tự hồi quy var ra, chúng ta có thể sử dụng thêm mô hình vecto hiệu chỉnh sai số vecm hay mô hình phân phối độ trễ adrl … để ước lượng vấn đề này.
Các bước thực hiện trên phần mềm eviews
Để ước lượng mô hình tự hồi quy var chúng ta có thể sử dụng nhiều phần mềm khác nhau, điều cho ra kết quả giống nhau, trong bài này chúng tôi sẽ sử dụng phần mềm eviews để thực hiện ước lượng.
Thay vì, nói chung chung luanvanhay sẽ áp dụng thực tế vào số liệu thực tế để cho các bạn dễ hình dung. Chúng tôi sẽ dụng chung bộ dữ liệu trong phần tìm chuỗi dùng và đồng liên kết. Trong phần này cũng có phần về chuỗi dừng và đồng liên kết các bạn muốn hiểu rõ vui lòng xem lại bài này, chúng tôi thực hiện trê phần mềm stata, nên tương đối dễ hiểu hơn là phần mềm views.
Vì vậy, chúng ta sẽ khảo sát: GIADV = KCACH + SLAU
Giá đơn vị = khoảng cách + số lầu.
Đây là bộ dữ liệu, mình trích các biến ra để phục vụ bài này, đó là dữ liệu về các tính giá nhà. ( Các bạn cũng chẳng cần quan tâm)
Bước 1: Kiểm tra các dữ liệu đưa vào đã dừng ( ổn định) hay chưa ?
Mình nhắc lại là các bạn nên xem lại bài cách tính chuỗi dừng.
Mở biến > Menu View > Unit Root Test
Ta xem biến GIADV
Bài mới !
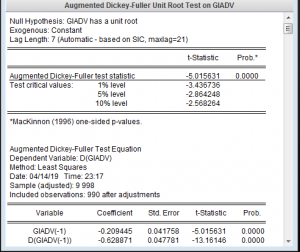
ta có chuỗi GIADV đã ổn định khi không cần sai phân
Còn biến khoảng cách
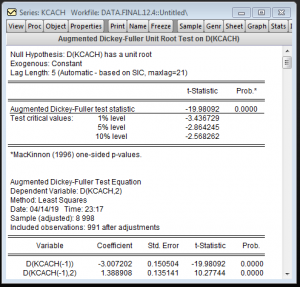
Dữ liệu KCACH đã ổn định khi sai phân bậc 1.
Cuối cùng ta xem dữ liệu SLAU
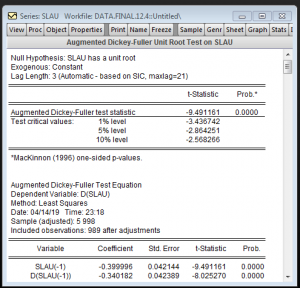
Trong dữ liệu SLAU thì đã dừng không cần sai phân.
Vì vậy, chúng ta có biến KCACH phải sai phân bậc 1 để ổn định, Như vậy chúng ta không thể nào áp dụng được mô hình hồi quy ols được; Nên chúng ta sử dụng mô hình tự hồi quy var để áp dụng vào mô hình.
Bước 2: Lựa chọn lag phù hợp cho mô hình
Trong bảng kết quả hồi quy var ta chọn
View > Lag Structure > Lag lenght criteria
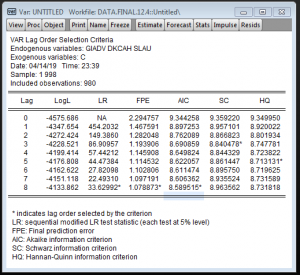
Cách chọn lag các bạn làm như sau: trong hình những hàng nào có dấu (*) là có lag ở đó, nếu trong mô hình chúng ta có nhiều (*) thì chọn AIC nhỏ nhất. Với điều kiện này thì mô hình chúng ta lag phù hợp là 5.
Chúng ta có độ trễ lag rồi, giờ chúng ta chạy mô hình tự hồi quy var
Bước 3: Chạy mô hình VAR trên views
Quick > Estimate VAR
Mục VAR type chọn: Standard VAR
Trong hộp thoại Endogenous: Chúng ta đưa các biến GIADV DKCACH SLAU vào
Chổ Lag tao chọn 1 -5
Chú ý tạo biến DKCACH: genr DKCACH = d(KCACH)
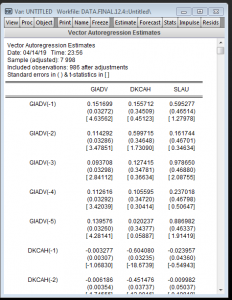
Ta được kết quả hồi quy var như trên.
Khi được kết quả như trên chúng ta chưa thể sử dụng được, mà chúng ta cần kiểm định thêm vài thứ:
Bước 4: Kiểm định Granger
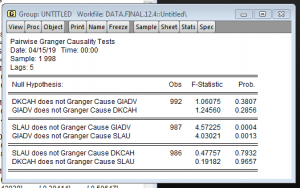
Sau khi kiểm định Granger thì chúng ta chỉ có sự tác động qua lại giữa GIADV với SLAU.
Bước 5: Kiểm định phân dư có bị tự tương quan không ?
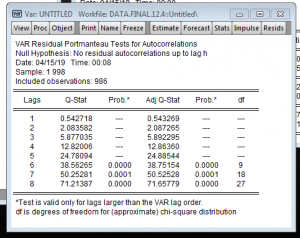
Từ kiểm định trên thì dữ liệu của chúng ta có tự tương quan
Bước 6 kết quả hồi quy var
Chúng ta giả sử dữ liệu của chúng ta không bị sai phạm gì hết chúng ta có kết quả như sau:
GIADV = 0.151699398683*GIADV(-1) + 0.114291845344*GIADV(-2) + 0.0937075260825*GIADV(-3) + 0.112616083278*GIADV(-4) + 0.139575667958*GIADV(-5) – 0.00327718340659*DKCAH(-1) – 0.00618576407935*DKCAH(-2) – 0.00207722916939*DKCAH(-3) – 0.00447482873956*DKCAH(-4) – 0.00379177383655*DKCAH(-5) + 0.007898590094*SLAU(-1) + 0.000642394546714*SLAU(-2) + 0.00221776174808*SLAU(-3) + 0.00413140561862*SLAU(-4) + 0.000255393712925*SLAU(-5) + 0.0366815240787
Trên đây là một ví dụ về mô hình tự hồi quy var, do dự liệu để áp dụng mô hình này chúng ta cần phải đưa những biến có độ nhạy cao vào như nói ở trên, do gấp quá nên chúng tôi không chuẩn bị được dữ liệu tốt, nên kết quả hồi quy không được đẹp, (chúng tôi lấy ngẫu nhiên từ bộ dữ liệu đang làm) nên chúng ta cần phải xử lý lại dữ liệu./.
