Ước lượng tác động hài hạn hồi quy FMOLS Fully Modified Ordinary Least làm một trong những mô hình định lượng quan trọng trong kinh tế, nhằm ước lược hiệu quả tác động dài hạn, song song với FM-OLS chúng ta còn có hồi quy DOLS và CCR, trong đó hồi quy ước lượng dài hạn FMOLS được sử dụng rộng rãi và nhiều nhất.
ƯỚC LƯỢNG TÁC ĐỘNG DÀI HẠN FMOLS
Hồi quy bình phương nhỏ nhất hồi quy FMOLS
Hồi quy bình phương nhỏ nhất (FM-OLS) được sửa đổi hoàn toàn ban đầu được thiết kế bởi Phillips và Hansen (1990) để cung cấp các ước lượng tối ưu về hồi quy đồng liên kết. Phương pháp điều chỉnh bình phương nhỏ nhất để tính đến các hiệu ứng tương quan nối tiếp và tính nội sinh trong các bộ hồi quy là kết quả của sự tồn tại của mối quan hệ đồng liên kết. Bài báo này cung cấp một khuôn khổ chung giúp có thể nghiên cứu hành vi tiệm cận của FM-OLS trong các mô hình có đầy đủ các bộ hồi quy cấp I (1), các mô hình với các bộ hồi quy I (1) và I (0), các mô hình có gốc đơn vị và các mô hình chỉ với các bộ hồi quy tĩnh.
Khung này cho phép chúng tôi xem xét việc sử dụng hồi quy FM trong bối cảnh tự động hồi quy vectơ (VAR) với một số gốc đơn vị và một số quan hệ đồng liên kết. Các hồi quy FM-VAR kết quả được hiển thị có một số đặc tính thú vị. Ví dụ, khi có một số đồng liên kết trong hệ thống, ước lượng FM-VAR có một lý thuyết giới hạn là chuẩn cho tất cả các hệ số đứng yên và chuẩn hỗn hợp cho tất cả các hệ số không cố định. Do đó, không có phân phối giới hạn căn đơn vị ngay cả trong trường hợp của hệ số căn đơn vị con submatrix , đối với VAR n chiều với r vectơ đồng liên kết). Hơn nữa, ước tính tối ưu của không gian đồng liên kết đạt được trong hồi quy FM-VAR mà không cần biết trước về số lượng gốc đơn vị trong hệ thống, mà không cần xác định thứ nguyên của không gian đồng liên kết và không sử dụng các kỹ thuật hồi quy hạn chế như hồi quy cấp bậc giảm .
Phát triển của FM-OLS lên FM-VAR
Nghiên cứu cũng phát triển một lý thuyết tiệm cận để suy luận dựa trên hồi quy FM-OLS và FM-VAR. Lý thuyết giới hạn cho các bài kiểm tra Wald dựa trên công cụ ước lượng FM được chỉ ra là liên quan đến sự kết hợp tuyến tính của các biến chi bình phương độc lập. Phân phối giới hạn này được giới hạn ở trên bởi phân phối chi bình phương thông thường với bậc tự do bằng số giới hạn. Do đó, các giá trị tới hạn thông thường có thể được sử dụng để xây dựng các phép thử tiệm cận hợp lệ (nhưng thận trọng) trong các phép hồi quy chuỗi thời gian FM khá tổng quát.
Lý thuyết này áp dụng cho kiểm tra quan hệ nhân quả trong VAR và do đó có khả năng hữu ích trong các ứng dụng thực nghiệm. các giá trị tới hạn thông thường có thể được sử dụng để xây dựng các phép thử tiệm cận hợp lệ (nhưng thận trọng) trong các phép hồi quy chuỗi thời gian FM khá tổng quát. Lý thuyết này áp dụng cho kiểm tra quan hệ nhân quả trong VAR và do đó có khả năng hữu ích trong các ứng dụng thực nghiệm. các giá trị tới hạn thông thường có thể được sử dụng để xây dựng các phép thử tiệm cận hợp lệ (nhưng thận trọng) trong các phép hồi quy chuỗi thời gian FM khá tổng quát. Lý thuyết này áp dụng cho kiểm tra quan hệ nhân quả trong VAR và do đó có khả năng hữu ích trong các ứng dụng thực nghiệm.
Ước lượng FMOLS trên Eviews
Để ước lượng hồi quy fmols trên eviews ta đi theo đường dẫn sau:
Ta chọn tất cả những biến như thường lệ và mở theo as equation, nó hiện lên bảng equation Estimation ta chọn hộp thoại method: Coint regress , ta để mặc định fully – modified OLS, ta sẽ có kết quả output như sau:
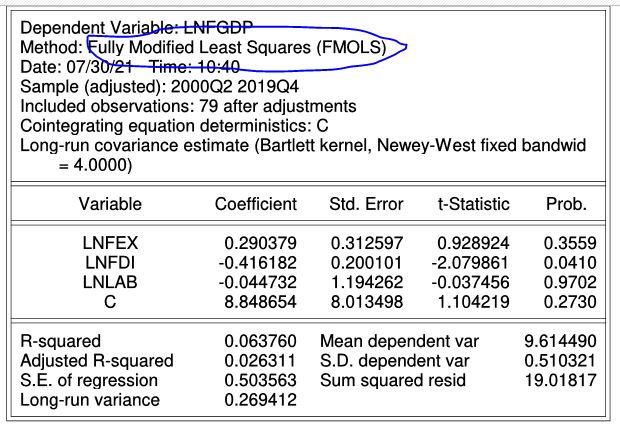
Ước lượng FMOLS trên Stata
Tiếp đến ta hồi quy mols trên Stata, việc hồi quy này cũng diễn ra đơn giản và dễ dàng, không có gì khó khăn ta dùng lệnh cointreg, và được kết quả như sau:
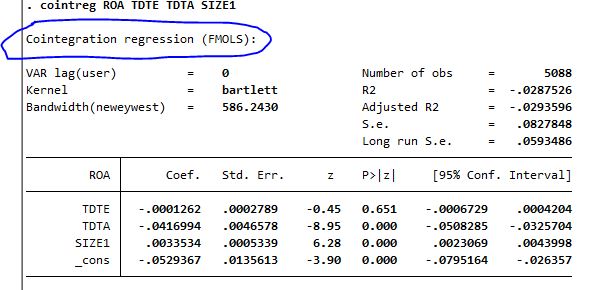
Ước lượng FMOLS trên R
Tiếp theo ta ước lượng fmols trên R, trong R thì có rất nhiều gói để ước lượng được điều này, ta có thể dùng gói cointreg ước lượng fmols, dols, ccr trong R.
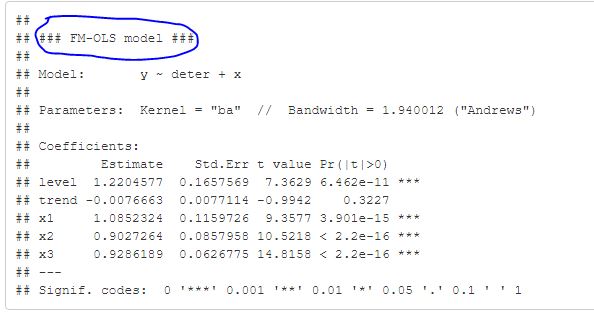
Trên đây là chúng ta vừa ước lượng FMOLS trên các phần mềm thống kê chuyên dụng EViews, Stata, R. Các bạn làm quen với phần mềm nào thì dùng phần mềm ấy để ước lượng, làm sao cho mình dễ dàng nhất là được.















![[Mở lớp] Phân tích dữ liệu Stata Smartpls Amos R-studio SPSS Minitab NCSS](https://luanvanhay.org/wp-content/uploads/2023/05/huong-dan-6-120x86.jpg)

