Hồi quy đa thức Multinonimal Logistic Regression, đây là dạng hồi quy nhị phân logistic khi mở rộng biến phụ thuộc của mình lên nhiều hơn 2 giá trị, với việc ứng dụng rộng rãi không khác gì hồi quy nhị phân.

Hồi quy đa thức

Hồi quy đa thức là gì ?

Hồi quy logistic đa thức (thường được gọi là ‘hồi quy đa thức’) được sử dụng để dự đoán một biến phụ thuộc danh nghĩa cho một hoặc nhiều biến độc lập. Nó đôi khi được coi là một phần mở rộng của hồi quy logistic nhị thức để cho phép một biến phụ thuộc có nhiều hơn hai loại. Cũng như các loại hồi quy khác, hồi quy logistic đa thức có thể có các biến độc lập danh nghĩa và / hoặc liên tục và có thể có tương tác giữa các biến độc lập để dự đoán biến phụ thuộc.

Những ví dụ Multinonimal Logistic Regression

Ví dụ: bạn có thể sử dụng hồi quy logistic đa thức để hiểu người tiêu dùng thích loại đồ uống nào dựa trên vị trí ở Vương quốc Anh và độ tuổi (nghĩa là, biến phụ thuộc sẽ là “loại đồ uống”, với bốn danh mục – Cà phê, Nước ngọt, Trà và Nước – và các biến độc lập của bạn sẽ là biến danh nghĩa, “vị trí ở Vương quốc Anh”, được đánh giá bằng ba loại – London, Nam Vương quốc Anh và Bắc Vương quốc Anh – và biến liên tục, “tuổi”, được đo bằng năm).

Ngoài ra, bạn có thể sử dụng hồi quy logistic đa thức để hiểu liệu các yếu tố như thời hạn làm việc trong công ty, tổng thời gian làm việc, trình độ và giới tính có ảnh hưởng đến vị trí công việc của một người hay không (nghĩa là, biến phụ thuộc sẽ là “vị trí công việc”, với ba loại – cơ sở ban quản lý,

Các giả định của hồi quy

Khi bạn chọn phân tích dữ liệu của mình bằng hồi quy logistic đa thức, một phần của quy trình bao gồm việc kiểm tra để đảm bảo rằng dữ liệu bạn muốn phân tích thực sự có thể được phân tích bằng cách sử dụng hồi quy logistic đa thức. Bạn cần làm điều này vì chỉ thích hợp sử dụng hồi quy logistic đa thức nếu dữ liệu của bạn “vượt qua” sáu giả định cần thiết cho hồi quy logistic đa thức để cung cấp cho bạn một kết quả hợp lệ. Trên thực tế, việc kiểm tra sáu giả định này chỉ làm tăng thêm một chút thời gian cho phân tích của bạn, yêu cầu bạn nhấp thêm một vài nút trong Thống kê SPSS khi thực hiện phân tích, cũng như suy nghĩ thêm một chút về dữ liệu của bạn, nhưng nó là không phải là một nhiệm vụ khó khăn.

Đọc thêm: Đề tài nghiên cứu khoa học là gì ?

Trước khi chúng tôi giới thiệu cho bạn sáu giả định này, đừng ngạc nhiên nếu khi phân tích dữ liệu của riêng bạn bằng Thống kê SPSS, một hoặc nhiều giả định này bị vi phạm (tức là không được đáp ứng). Điều này không có gì lạ khi làm việc với dữ liệu trong thế giới thực hơn là các ví dụ trong sách giáo khoa, thường chỉ cho bạn thấy cách thực hiện hồi quy logistic đa thức khi mọi thứ diễn ra tốt đẹp! Tuy nhiên, đừng lo lắng. Ngay cả khi dữ liệu của bạn không đạt được các giả định nhất định, thường có một giải pháp để khắc phục điều này. Đầu tiên, chúng ta hãy xem xét sáu giả định sau:

HOT:

Biến phụ thuộc là biến danh nghĩa ( Rời rạc)

Giả định số 1: Biến phụ thuộc của bạn nên được đo lường ở mức danh nghĩa . Ví dụ về các biến danh nghĩa bao gồm sắc tộc (ví dụ: với ba loại: Da trắng, Mỹ gốc Phi và Tây Ban Nha), loại phương tiện giao thông (ví dụ: với bốn loại: xe buýt, ô tô, xe điện và xe lửa), nghề nghiệp (ví dụ: với năm nhóm: bác sĩ phẫu thuật, bác sĩ , y tá, nha sĩ, bác sĩ trị liệu), v.v. Hồi quy logistic đa thức cũng có thể được sử dụng cho các biến thứ tự , nhưng thay vào đó bạn có thể cân nhắc chạy hồi quy logistic thứ tự . Bạn có thể tìm hiểu thêm về các loại biến trong bài viết của chúng tôi: Các loại biến .

Biến độc lập

Giả định số 2: Bạn có một hoặc nhiều biến độc lập liên tục , thứ tự hoặc danh nghĩa (bao gồm cả các biến phân đôi ). Tuy nhiên, các biến độc lập thứ tự phải được coi là liên tục hoặc phân loại. Chúng không thể được coi là biến thứ tự khi chạy hồi quy logistic đa thức trong Thống kê SPSS; một cái gì đó chúng tôi đánh dấu sau trong hướng dẫn. Ví dụ về các biến liên tục bao gồm tuổi (đo bằng năm), thời gian ôn tập (đo bằng giờ), thu nhập (đo bằng đô la Mỹ), trí thông minh (đo bằng điểm IQ), thành tích thi (đo từ 0 đến 100), cân nặng (đo bằng kg), v.v.

Ví dụ vềcác biến thứ tự bao gồm các mục Likert (ví dụ: thang điểm 7 từ “rất đồng ý” đến “rất không đồng ý”), trong số các cách xếp hạng danh mục khác (ví dụ: thang điểm 3 giải thích mức độ thích một sản phẩm của khách hàng, từ “Không nhiều lắm”, thành “Cũng được”, thành “Có, rất nhiều”). Các biến danh nghĩa ví dụ đã được cung cấp trong gạch đầu dòng trước đó.

Đọc thêm: hồi quy biến công cụ khắc phục nội sinh

Độc lập của quan sát

Giả định số 3: Bạn nên có sự độc lập của các quan sát và biến phụ thuộc phải có các danh mục loại trừ lẫn nhau và đầy đủ .

Đa cộng tuyến

Giả định số 4: Không được có đa cộng tuyến . Đa cộng tuyến xảy ra khi bạn có hai hoặc nhiều biến độc lập có tương quan cao với nhau. Điều này dẫn đến các vấn đề trong việc hiểu biến nào góp phần giải thích biến phụ thuộc và các vấn đề kỹ thuật trong tính toán hồi quy logistic đa thức. Xác định xem có đa cộng tuyến hay không là một bước quan trọng trong hồi quy logistic đa thức. Thật không may, đây là một quá trình đầy đủ trong Thống kê SPSS yêu cầu bạn tạo bất kỳ biến giả nào cần thiết và chạy nhiều thủ tục hồi quy tuyến tính.

Quan hệ tuyến tính

Giả thiết số 5: Cần có mối quan hệ tuyến tính giữa bất kỳ biến độc lập liên tục nào và phép biến đổi logit của biến phụ thuộc .

Quan sát ngoại vi

Giả định số 6: Không được có ngoại lệ , giá trị đòn bẩy cao hoặc các điểm có ảnh hưởng lớn .

Bạn có thể kiểm tra các giả định # 4, # 5 và # 6 bằng cách sử dụng Thống kê SPSS. Các giả định # 1, # 2 và # 3 nên được kiểm tra trước, trước khi chuyển sang các giả định # 4, # 5 và # 6. Chỉ cần nhớ rằng nếu bạn không chạy thử nghiệm thống kê trên các giả định này một cách chính xác, kết quả bạn nhận được khi chạy hồi quy logistic đa thức có thể không hợp lệ.

Chạy hồi quy đa thức trên SPSS

Kích hoạt chạy chương trình

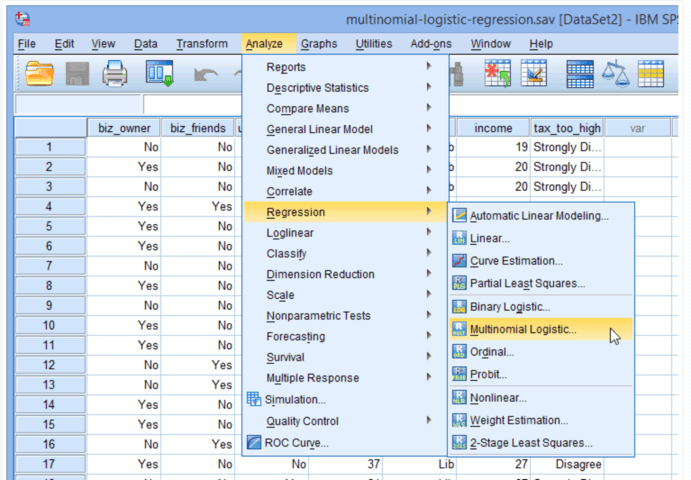
Analyze> Regression> Multinomial Logistic …

Và cấu hình như trong hình dưới:

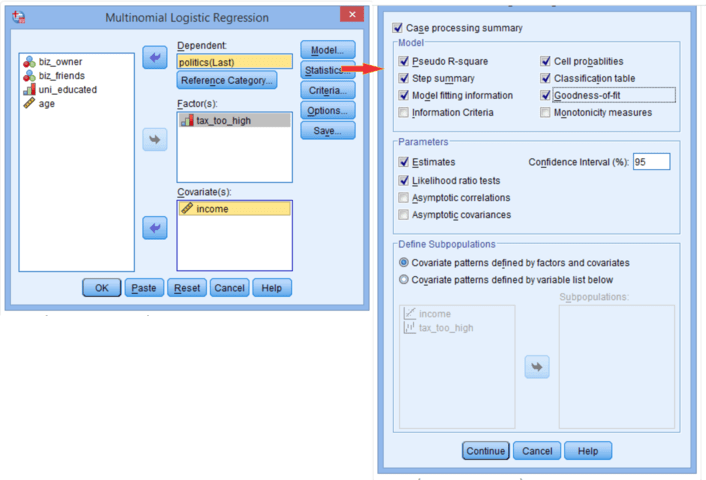
Trong cửa sổ hồi quy:

Đưa biến phụ thuộc vào ô dependent
Đưa biến độc lập là rời rạc vào ô factor
Đưa biến độc lập là liên tục vào ô Covariate

Trong các tab cấu hình, chúng ta chỉ chọn Statistic còn lại thì để mặc định, trong tab statistic thì chọn như hình trên.

Luận giải kết quả:

Đánh giá dữ liệu phù hợp với mô hình

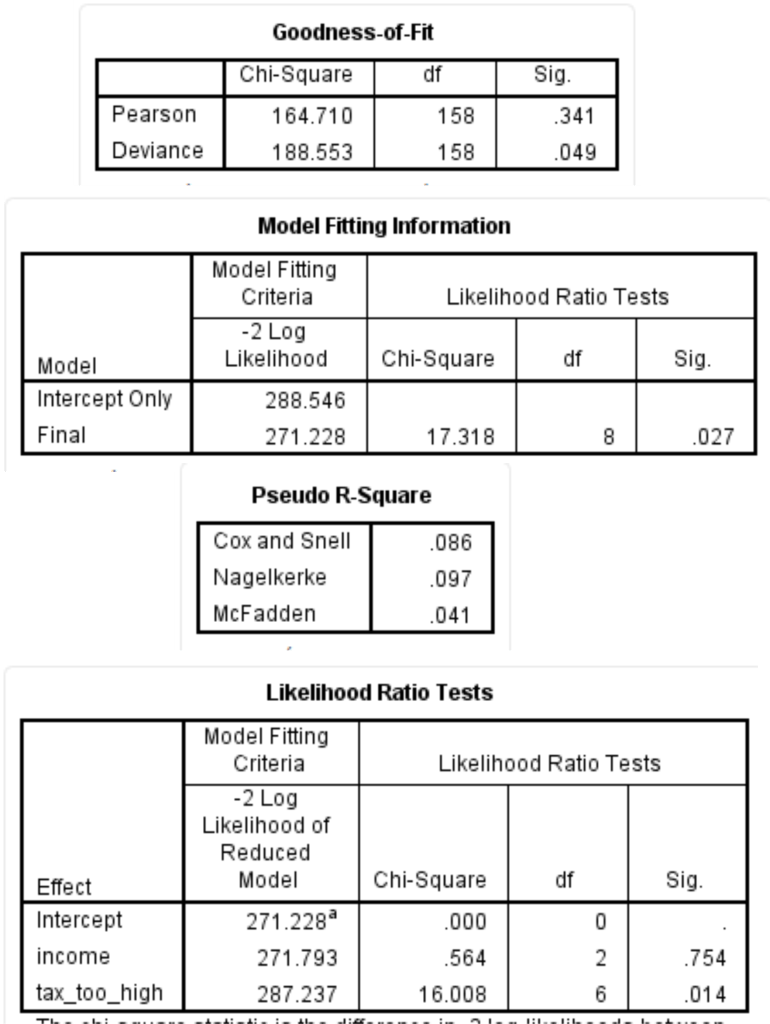
Trong bảng Goodness of fit

Hàng đầu tiên, có nhãn ” Pearson “, trình bày thống kê chi bình phương Pearson. Các giá trị chi-square lớn (được tìm thấy trong cột ” Chi-Square “) cho biết mô hình không phù hợp. Một kết quả có ý nghĩa thống kê (nghĩa là p <0,05) chỉ ra rằng mô hình không phù hợp với dữ liệu. Bạn có thể thấy từ bảng trên rằng giá trị p là .341 (tức là p = .341) (từ cột ” Sig. “) Và do đó, không có ý nghĩa thống kê. Dựa trên thước đo này, mô hình phù hợp với dữ liệu. Hàng còn lại của bảng (tức là hàng ” Độ lệch “) trình bày thống kê chi-bình phương Độ lệch.

Đọc thêm: nguyên nhân làm TFP thay đổi

Các biến không đồng thời bằng 0

Kết quả trong bảng Model fitting information

Hàng ” Cuối cùng ” trình bày thông tin về việc liệu tất cả các hệ số của mô hình có bằng 0 hay không (tức là, liệu bất kỳ hệ số nào có ý nghĩa thống kê hay không). Một cách khác để xem xét kết quả này là liệu các biến mà bạn đã thêm vào có cải thiện đáng kể về mặt thống kê so với một mình vùng chặn hay không (tức là không có biến nào được thêm vào). Bạn có thể thấy từ cột ” Sig. ” Rằng p = .027, có nghĩa là mô hình đầy đủ dự đoán có ý nghĩa thống kê về biến phụ thuộc tốt hơn so với mô hình chỉ đánh chặn một mình.

Tỉ lệ giải thích của mô hình

Trong hồi quy logistic đa thức, bạn cũng có thể xem xét các số đo tương tự như R ² trong hồi quy tuyến tính bình phương nhỏ nhất thông thường, là tỷ lệ phương sai có thể được giải thích bằng mô hình. Tuy nhiên, trong hồi quy logistic đa thức, đây là các số đo R ² giả và có nhiều hơn một, mặc dù không có giá trị nào có thể diễn giải dễ dàng. Tuy nhiên, chúng được tính toán và hiển thị bên dưới trong bảng Pseudo R-Square

Phân tích kết quả hồi quy

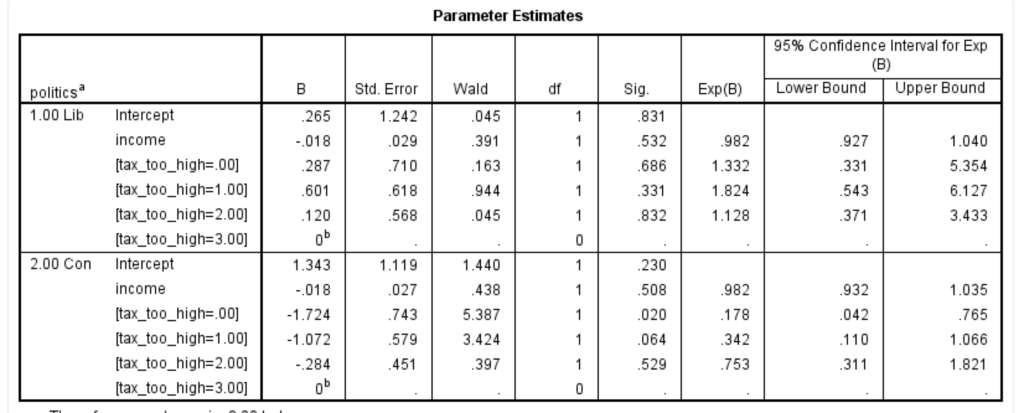
Bảng này trình bày các ước lượng tham số (còn được gọi là các hệ số của mô hình). Như bạn có thể thấy, mỗi biến giả có một hệ số cho biến tax_too_high. Tuy nhiên, không có giá trị ý nghĩa thống kê tổng thể. Điều này đã được trình bày trong bảng trước (ví dụ: Kiểm tra tỷ lệ khả năng bàn). Vì có ba loại biến phụ thuộc, bạn có thể thấy rằng có hai bộ hệ số hồi quy logistic (đôi khi được gọi là hai logits). Tập hợp hệ số đầu tiên được tìm thấy trong hàng “Lib” (đại diện cho sự so sánh của danh mục Đảng Dân chủ Tự do với danh mục tham chiếu, Lao động). Bộ hệ số thứ hai được tìm thấy trong hàng “Con” (lần này đại diện cho sự so sánh của danh mục Bảo thủ với danh mục tham chiếu, Lao động). Bạn có thể thấy rằng “thu nhập” cho cả hai bộ hệ số không có ý nghĩa thống kê ( p = .532 và p = .508 tương ứng; cột ” Sig. “).

Hệ số duy nhất (cột ” B “) có ý nghĩa thống kê dành cho tập hợp hệ số thứ hai. Nó là [tax_too_high = .00] ( p = .020), là một biến giả thể hiện sự so sánh giữa “Hoàn toàn không đồng ý” và “Hoàn toàn đồng ý” với mức thuế quá cao. Dấu hiệu là tiêu cực, cho thấy rằng nếu bạn “rất đồng ý” so với “rất không đồng ý” rằng mức thuế quá cao, bạn có nhiều khả năng Bảo thủ hơn Lao động. Tuy nhiên, bởi vì hệ số không có cách giải thích đơn giản, thay vào đó, các giá trị lũy thừa của hệ số (cột ” Exp (B) “) thường được xem xét.

Tags: đa thức độc lập hồi quy phụ thuộc tham số